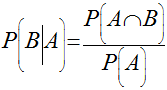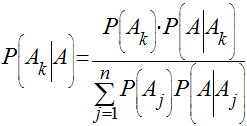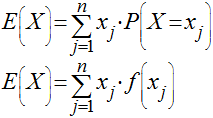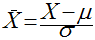Estatística Aplicada à Geração de Energia
A estatística possui um grande papel na geração de energia elétrica e, por isso, merece um capítulo de revisão neste curso.
A demanda de energia, a água nas hidrelétricas, o sol na geração solar e os ventos, que acionam turbinas eólicas e provocam a dispersão de poluentes na atmosfera, apresentam um comportamento randômico que só a estatística pode explicar.
Espaço de Amostragem
Espaço de amostragem – S - é o conjunto de todos os possíveis resultados de um experimento randômico.
Eventos
Evento é um subconjunto A é um subconjunto do espaço de amostragem S. Quando este subconjunto é unitário ele é chamado de evento elementar ou simples.
Probabilidade
Se um evento – A - pode ocorrer de h maneiras diferentes de um total de n possibilidades diferentes e igualmente prováveis, sua probabilidade P(A) é definida como sendo h/n.
Se após n repetições de um experimento, onde n é um número suficientemente grande, um determinado evento A ocorreu h vezes, a probabilidade também é definida como sendo P(A)=h/n.
Matematicamente, pode-se definir a probabilidade como sendo:
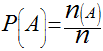
onde:
n(A) é o número de ocorrências do evento A;
n é o número total de eventos.
Axiomas
1. Para todo Evento A, P(A)≥0
2. Para todo e qualquer evento A, 0≤P(A)≤1
3. P(A)=1 implica A é um evento certo.
4. P(A)=0 implica que o evento A é impossível de ocorrer.
6. Se o Evento A’ é o complemento de A, então P(A’)=1-P(A)
7. Para quaisquer dois eventos A e B, teremos que:
.gif)
9. Somatório ou integral das probabilidades de todos os eventos de um espaço S é igual a 1.
.gif)
Probabilidade Condicional
Sejam A e B dois eventos de um espaço S com probabilidades maiores que zero. A probabilidade de B ocorrer dado que A ocorre é dada pela expressão abaixo.
Lei de Bayes
Supondo A1, A2,....., An, eventos mutuamente exclusivos cuja união forma o espaço de amostragem S, isto é, um deles deve obrigatoriamente ocorrer a Lei de Bayes diz que:
Eventos Independentes
Dois eventos são estatisticamente independentes se:
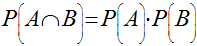
Três eventos são independentes se eles forem independentes dois a dois e se:
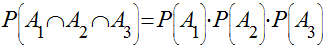
Função Probabilidade ou Distribuição de Probabilidade
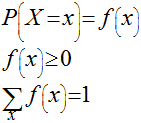
Função de Distribuição Acumulada ou Função de Distribuição
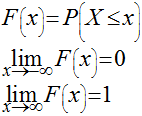
Valor Esperado ou Média
No caso das probabilidades serem iguais, o valor esperado é igual à média aritmética. Quando isso não ocorre, duas outras medidas são utilizadas; a moda e a mediana. O valor esperado também é chamado de média - μ.
Moda
A moda é de uma variável randômica é o valor que ocorre com maior freqüência ou com maior probabilidade. Algumas vezes, existem variáveis randômicas com mais de um valor muito freqüente. Neste caso, a função de distribuição é chamada de bimodal ou multimodal.
Mediana
A mediana é o valor da variável randômica que separa a função de distribuição em duas metades iguais.
Teoremas Sobre Valor Esperado
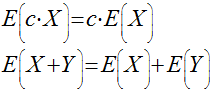
Se, e apenas se, X e Y forem variáveis randômicas independentes, teremos que:
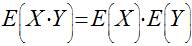
Momento de Ordem r
Existem casos especiais de momentos que fornecem informações importantes sobre as variáveis randômicas.
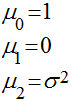
Distorção (Skewness)
A distorção mede o grau de assimetria da distribuição de uma variável aleatória e definida como sendo:
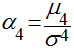
A Distorção pode ser positiva ou negativa conforme a distorção seja para a direita ou esquerda respectivamente. Distorção igual a zero significa uma distribuição perfeitamente simétrica, como a distribuição normal.
Curtose (Kurtosis)
A curtose mede o quanto a distribuição da variável aleatória é mais plana ou não e é dada por:
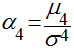
Valores maiores do que 3, que é o valor da distribuição normal, representam distribuições com picos elevados e valores menores do que 3 representam distribuições mais planas.
Variância e Desvio Padrão
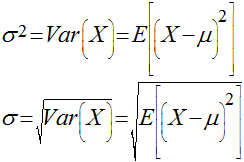
Teoremas Sobre Variância
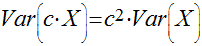
Se, e somente se, X e Y forem variáveis randômicas independentes, teremos que:
Normalização de Variáveis Aleatórias
Dada uma variável aleatória com média μ e desvio padrão σ, a variável pode ser transformada em uma variável aleatória estandardizada da seguinte maneira:
Covariância
Considerando duas variáveis aleatórias X e Y com função densidade de probabilidade igual a f(x,y), teremos que:
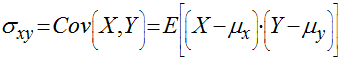
Se X e Y são variáveis randômicas independentes, a covariância é igual a zero.
Fator de Correlação
Portanto, o fator de correlação entre duas variáveis aleatórias é dado por:
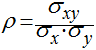
O fator de correlação varia entre -1, negativamente correlacionado e 1, positivamente correlacionado. Um fator de correlação zero significa que as variáveis são independentes.
Funções de Distribuição
Distribuição de Binomial
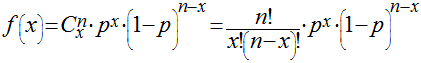
Esta distribuição representa a probabilidade de um evento, com probabilidade p de ocorrer e q (igual a 1-p) de não ocorrer, ocorrer x vezes em n tentativas. No caso especial de n=1, esta distribuição se transforma na Distribuição de Bernoulli. Esta Figura mostra a função da probabilidade Binomial. A média, variância, distorção e curtose são dados abaixo.
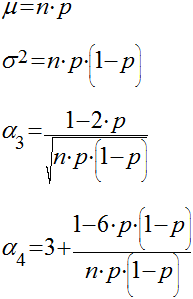
Distribuição Normal ou Gaussiana
A distribuição normal é uma das distribuições mais conhecidas e utilizadas.
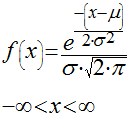
Distribuição Lognormal
Na prática, muitas distribuições de probabilidade possuem inclinação devido a leis da física que governam o tipo de evento analisado. Diversos fenômenos físicos, tais como vento, precipitação e vazão, não possuem valores negativos mas não possuem limitações superiores. Isto faz com a distribuição estatística dessas grandezas apresente uma inclinação para a direita e, por isso, não podem ser aproximados pela distribuição normal. No entanto, o logaritmo dessas grandezas pode ser aproximado pela distribuição normal. Daí resulta a Distribuição Lognormal.
Histogramas
O Histograma é a forma de se obter, a partir de um conjunto de dados, a distribuição estatística desta amostra.