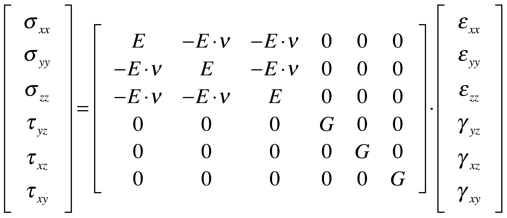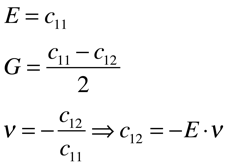Materiais Elétricos e Magnéticos
II. Propriedades dos Materiais
Onde:
-
•ρ é a densidade do material [kg/m3];
-
•m é a massa do corpo [kg];
-
•V é o volume do corpo [m3];
Portanto, a densidade é uma grandeza escalar, tensor de ordem zero, que depende apenas do material.
Tensão Mecânica
Por isso, define-se Tensão Mecânica como sendo:




Propriedades Mecânicas

As propriedades mecânicas são fundamentais em todos os projetos e são:
-
•Densidade;
-
•Elasticidade;
-
•Ductilidade;
-
•Resiliência;
-
•Tenacidade.

Densidade
O peso é sempre fator importante em projetos de engenharia, mesmo em projetos de equipamentos elétricos, eletrônicos e de telecomunicação.
Contudo, peso é uma grandeza macroscópica que depende do material e das dimensões do corpo em questão.
Por isso, no estudo dos materiais, procura-se separar as propriedades dos materiais das formas e dimensões do corpo.
Para isso, define-se densidade como sendo:

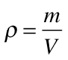
Este é o momento ideal de fazer o Trabalho de Cabos, o Trabalho de Elasticidade e o Trabalho de Inosotropia.
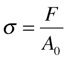
Onde:
-
•σ é a tensão mecânica [MPa];
-
•F é a força instantânea perpendicular à seção transversal [N];
-
•A0 é a área original da seção transversal [m2].
Por outro lado, define-se Deformação Mecânica como sendo:
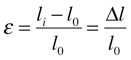
Onde:
-
•ε é a Deformação;
-
•li é o comprimento instantâneo [m];
-
•l0 é o comprimento original [m].
Desta maneira, a Deformação é adimensional e a Tensão Mecânica independe das dimensões do corpo.
As figuras abaixo mostram os efeitos da Tração e Compressão em corpos cilíndricos.
Quando submetidos à tração, os corpos alongam seu comprimento mas reduzem sua seção reta e o oposto ocorre quando submetidos a compressão. Esta é a primeira indicação que as propriedades dos materiais podem ser Anisotrópicas.
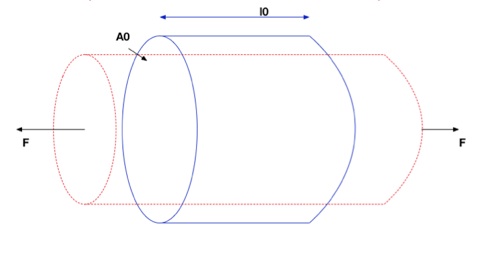
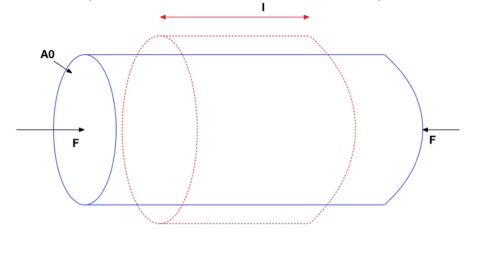
Compressão
Tração
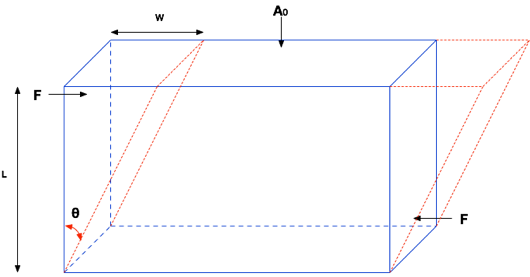
As forças nem sempre atuam no mesmo eixo. Quando isto ocorre, existe o fenômeno do Cisalhamento, conforme mostra a figura abaixo.
Cisalhamento
A Tensão de Cisalhamento é definida como sendo a Força de Cisalhamento dividida pela área do corpo na direção da força. Observe que a área considerada é perpendicular à considerada no caso da Tensão.
Por sua vez, a Deformação de Cisalhamento é definida como sendo a variação linear na direção da força divida pela dimensão perpendicular à força.
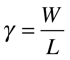
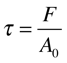
A Ductilidade mede o grau de deformação plástica até a fratura é definida como:
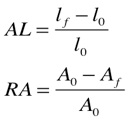
Onde:
-
•AL é o alongamento normalizado;
-
•RA é a redução de área ou Coeficiente de Estricção;
-
•l0 é o comprimento inicial;
-
•A0 é a área inicial;
-
•lf é o comprimento no momento da fratura;
-
•Af é a área no momento da fratura.
Materiais com pouca deformação plástica até a fratura, Ductilidade baixa, quebram rapidamente e, por isso, são chamados de frágeis.
Resiliência
Quando o material opera na região elástica, ele funciona como uma mola e toda a energia armazenada na compressão ou alongamento é recuperada após a remoção da carga.
O Módulo de Resiliência - Ur [Pa] - é dado pelas expressões abaixo em função da Tensão ou da Deformação.
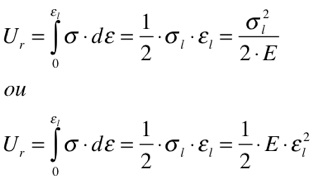
Tenacidade
A Tenacidade é a energia absorvida pelo material até sua fratura quando submetido a uma tensão mecânica. Portanto, a Tenacidade é uma Resiliência medida até a fratura. Como a Elasticidade não é constante até a Fratura, não existe uma expressão definida para a Tenacidade. Contudo, ela pode ser calculada numericamente a partir da expressão abaixo.
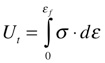

Este foi o trabalho nota 10 de 2013_1.
Parabéns Pedro e Isadora
Elasticidade
Outra propriedade mecânica muito importante é a Elasticidade. Ela representa a relação linear entre alongamento e força, como numa mola ou elástico.
Contudo, o alongamento depende da característica do material e das dimensões do corpo em questão.
A Elasticidade - c - é um tensor de quarta ordem e está relacionada com os tensores Tensão Mecânica e Deformação de acordo com expressão abaixo. O inverso da Elasticidade, “Compliance” - s- também é um tensor de quarta ordem.
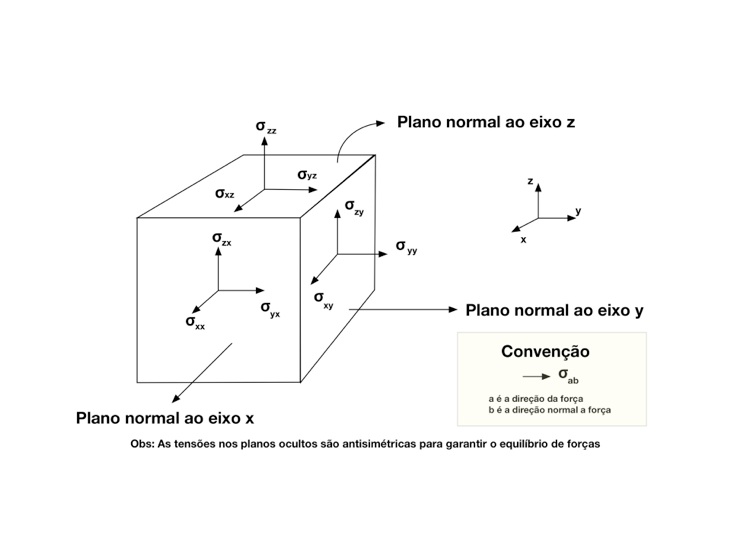
A figura abaixo apresenta as tensões em um volume cúbico unitário de material. Observa-se que existem três tensões em cada face do cubo: uma Tensão de Tração e duas Tensões de Cisalhamento. Por simplicidade, a figura mostra apenas três fases do cubo porque, para manter o equilíbrio de forças, as outras faces apresentam tensões iguais mas de direção contrária.
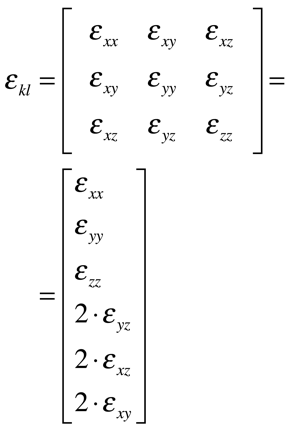
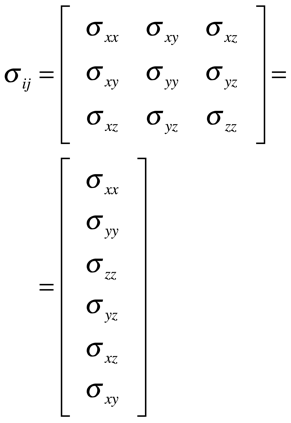
Em função disso, a Tensão Mecânica e a Deformação podem ser escritos como tensores de segunda ordem conforme a expressão abaixo.
No caso da Tensão Mecânica, o primeiro índice representa a direção da força e o segundo o plano normal. No caso da Deformação, o primeiro índice representa a direção do deslocamento e o segundo a direção do eixo de medição. Portanto, o sistema de eixos da Tensão não precisa ser o mesmo da Deformação.Contudo, em ambos os casos, os tensores são simétricos para manter o equilíbrio estático do corpo.
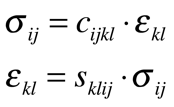
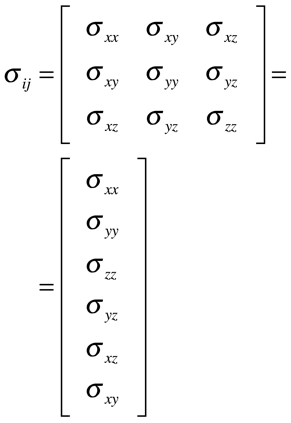
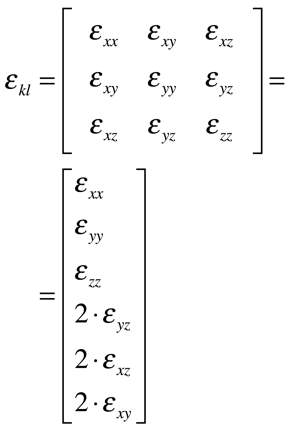
Em decorrência da simetria, os tensores Tensão Mecânica e Deformação podem ser escritos como vetores coluna da seguinte maneira:

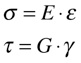
Onde:
-
•σ é a Tensão Mecânica [MPa];
-
•E é o Módulo de Elasticidade ou Módulo de Young [Mpa];
-
•G é o Módulo de Cisalhamento [MPa];
-
•τ é a Tensão de Cisalhamento;
-
•ε é a Deformação;
-
•ϒ é Deformação de Cisalhamento.
Portanto, os Módulos de Elasticidade e o Módulo de Cisalhamento estão relacionados com o Tensor de Elasticidade da seguinte maneira:
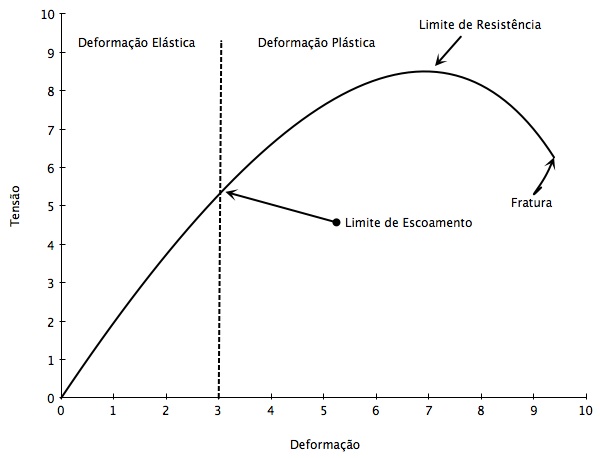
A figura abaixo mostra a relação entre Tensão e Deformação. Observa-se a região de deformação elástica, onde a relação da deformação-tensão é linear e outra, não linear, chamada de região de deformação plástica.
O aumento da tensão atinge seu ponto máximo no Limite de Resistência do Material e a Fratura ocorre no limite máximo de Deformação. É importante observa que eles não ocorrem simultaneamente.
Desta maneira, o Tensor Elasticidade pode ser escrito na forma matricial da seguinte maneira:
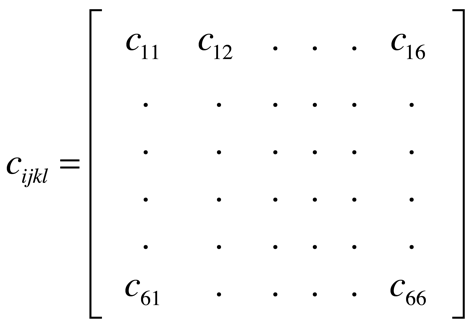
Contudo, em decorrência da densidade de energia elástica, esta matriz é simétrica e 21 coeficientes independentes são necessários para caraterizar completamente a elasticidade dos materiais.
Evidentemente, a medição desta quantidade de coeficientes não é trivial e, felizmente, não é necessária para muitos materiais nem para resolver todos os problemas.
Dependendo da estrutura atômica e molecular do material, o Tensor Elasticidade pode ser ainda mais simplificado. No caso de materiais isotrópicos, apenas 2 coeficientes são suficientes para caraterizar a Elasticidade do material, c11 e c12, conforme a expressão abaixo.
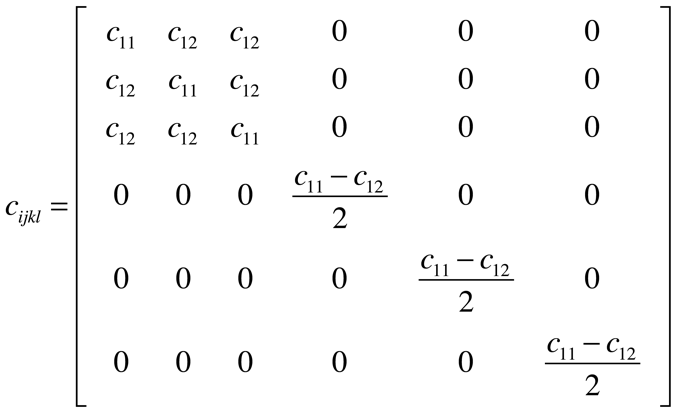
Por isso, o Fator de Anisotropia é definido como sendo:
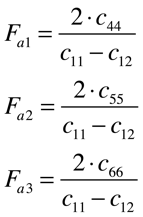
O material é considerado isotrópico quando os três fatores são iguais a 1. Neste caso, teremos que: