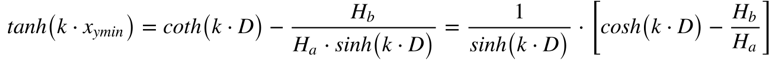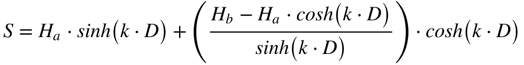A Catenária

Observe que os cabos de linhas de transmissão apresentam uma “barriga” que depende de diversos fatores, tais como:

1. • Peso do cabo;
   

2. • Temperatura do cabo;
   

3. • Distância entre as torres;
   

4. • Altura das torres;
   

5. • Tração no cabo.
   

Quem fez o trabalho de cabos, deve ter chegado a uma expressão do segundo grau para aproximar os pontos medidos.

Contudo, como podemos obter a equação do cabo utilizando a física e a matemática?

Considerando a referência dos eixos no ponto central da linha e analisando o equilíbrio de estático de forças da figura abaixo, teremos que:

Referências: Spiegel, M., Lipschutz, S., Liu, J., Manual de Tabelas e Fórmulas Matemáticas, Coleção Schaum, 3a edição, McGraw-Hill, 2009.

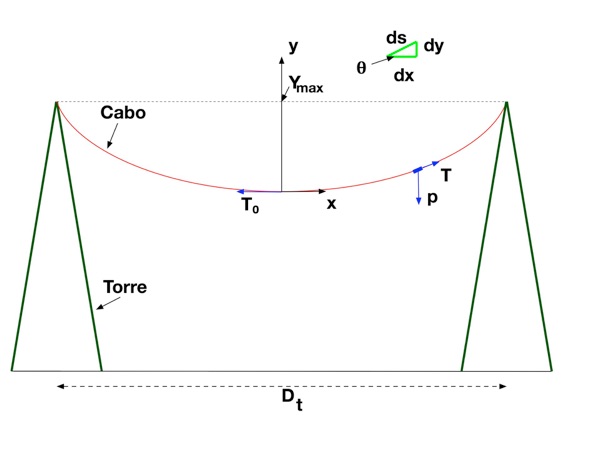
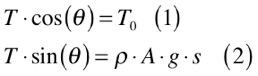
Onde:

1. •T é a força de tração no cabo [N];
   

2. •θ é o ângulo do cabo no ponto com relação aos eixos de referência;
   

3. •T0 é a tensão no cabo na origem do sistema de referência;
   

4. •ρ é a densidade do cabo [kg/m3];
   

5. •A é área da sção reta do cabo [m2];
   

6. •g é a aceleração da gravidade [m/s2];
   

7. •s é o comprimento do elemento do cabo [m].

Dividindo a equação (1) pela equação (2) e diferenciando com relação a x, obtemos a equação (3). Nesta passagem, consideramos que a área e a densidade do cabo são constantes.

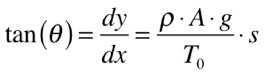
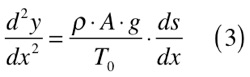
A partir da relação trigonométrica do triângulo verde da figura acima, podemos escrever que:

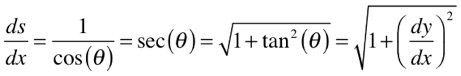
Substituindo este resultado na equação (3), obtêm-se a equação diferencial abaixo que relaciona y com x.

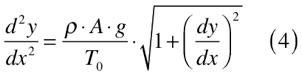
Como resolver esta equação diferencial?

A dica é usar o artifício da substituição de variáveis. Cria-se uma nova variável z, conforme a expressão abaixo, e substituindo na equação (4), teremos que:

Rearrumando a expressão anterior, passamos a ter uma equação diferencial com duas variáveis separadas, conforme a expressão abaixo.

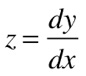
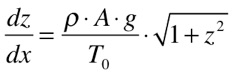
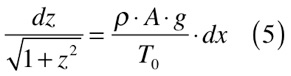
Duas equações com variáveis diferentes só poderão ser iguais no caso de serem constantes. Desta maneira, integrando as duas equações de acordo com Spiegel, teremos que:

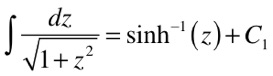
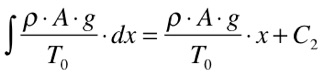
As constantes C1 e C2 dependem das condições iniciais do problema. Neste caso específico, de acordo com a figura acima, teremos que C1 é igual a C2 e a solução é a seguinte:

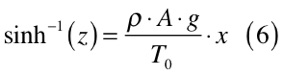
Arrumando a equação (6), teremos que:

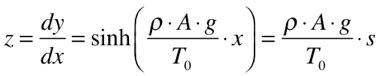
Portanto, o comprimento do cabo será dado por:

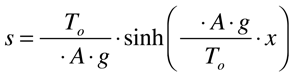
O comprimento total do cabo será dado, levando em consideração a simetria da figura, por:

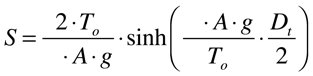
A constante To/(ρ.A.g) tem dimensão de comprimento e representa a força de tração dividida pelo peso do cabo por unidade de comprimento. Quando a distância entre as torres é muito pequena comparada com esta constante, o cabo fica praticamente esticado e sem barriga. Por outro lado, quando a distância entre as torres é muito maior do que esta constante, a barriga aumenta.

A altura y do cabo será dada por:

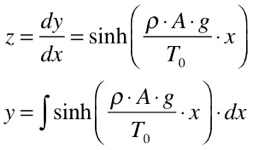
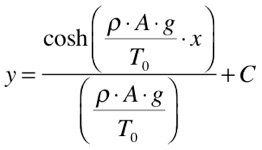
A constante C depende das condições de contorno do problema específico.

No caso em questão e de acordo com a figura acima, como y=0 pra x=0, a constante C e a altura y serão dados por:

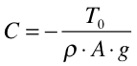
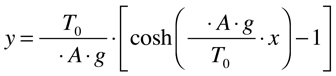
A flecha máxima, que representa a distância ymax, será dada, neste caso específico,  pela altura na torre:

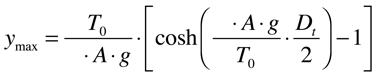
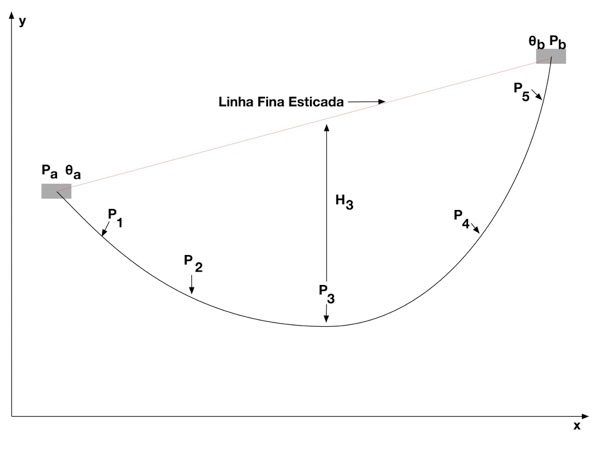
No caso geral de alturas de torre diferentes e a origem do eixo x em uma das torres, conforme a figura abaixo, a altura da linha será dada pela expressão abaixo:

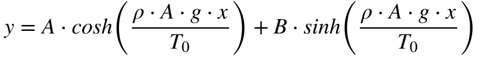
Considerando a altura da linha igual Ha para x=0 e Hb  para x=D (distância entre as torres), teremos que:

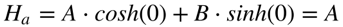
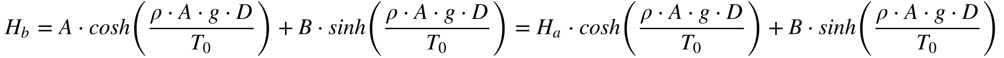
Portanto, a altura da linha será dada por:

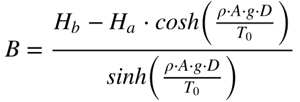
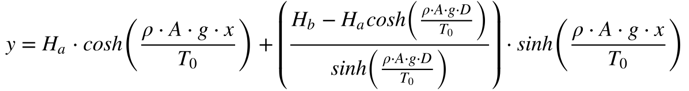
A altura será mínima quando a derivada da altura com relação a x for zero. Neste caso teremos que:

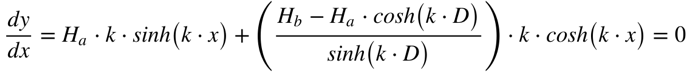
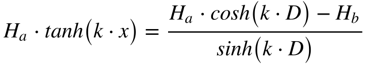
Onde:

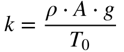
Conforme visto no início, a derivada do comprimento do cabo será dado por:

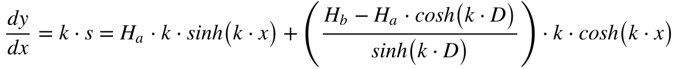
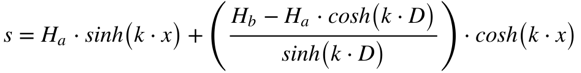
O comprimento total do cabo será dado por: