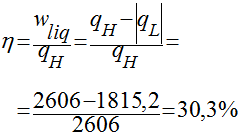Exemplos - Ciclo Rankine

Exemplo 1

Determine o rendimento de um ciclo Rankine, que utiliza água como fluido de trabalho, considerando que:

• A pressão no condensador é de 10 kPa;

• A pressão na caldeira é de 2 MPa;

• O vapor na saída da caldeira é saturado.

Solução

 

O rendimento é dado pela expressão abaixo.

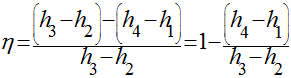
Para calcular o valor do rendimento térmico deste ciclo neste caso é necessário obter os valores das entalpias nos diversos pontos do ciclo. A Tabela abaixo apresenta os dados de entrada fornecidos pelo enunciado do problema. São dadas as pressões antes e depois da bomba - pontos 1 e 2 - e o título do vapor na saída da caldeira. Como o vapor é saturado, o título é 1.

A Tabela será preenchida de acordo com os passos abaixo utilizando o programa CATT2. Os valores em amarelo são os dados iniciais e os outros valores são calculados pelo programa a partir de 2 dados da linha da Tabela.

No ponto 1, pode-se considerar que a água encontra-se totalmente no estado líquido. Isto significa que seu título é zero.

Como o estado 1 é o único com dois dados, os cálculos começam neste estado. Os resultados obtidos com o programa estão em azul.

Ponto	Temperatura	Pressão	Entalpia	Entropia	Título	Volume
	°C	MPa	kJ/kg	kJ/kg/K		m3/kg
1	45,81	0,010	191,8	0,6492	0	0,00101
2		2
3					1
4

O próximo passo é determinar os dados do estado 2. O trabalho termodinâmico realizado pela bomba é dado por:

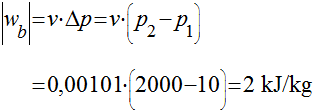
Onde:

v é o volume específico;

Δp é a variação de pressão na bomba.

Por outro lado, o trabalho realizado pela bomba também é igual à variação de entropia no fluido. Isto significa que:

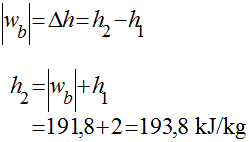
Considerando os dados em amarelo na Tabela abaixo como dados de entrada ao programa de cálculo de propriedades termodinâmicas, teremos que:

Ponto	Temperatura	Pressão	Entalpia	Entropia	Título	Volume
	°C	MPa	kJ/kg	kJ/kg/K		m3/kg
1	45,81	0,010	191,8	0,6492	0	0,00101
2	45,81	2	193,8	0,6491	Líquido comprimido	0,001009
3					1
4

Considerando a caldeira sem perdas, ela transfere calor para a água sem variar a pressão. Em função disso, podemos determinar todas as variáveis termodinâmicas do estado 3 conforme mostra a Tabela abaixo.

Ponto	Temperatura	Pressão	Entalpia	Entropia	Título	Volume
	°C	MPa	kJ/kg	kJ/kg/K		m3/kg
1	45,81	0,010	191,8	0,6492	0	0,00101
2	45,81	2	193,8	0,6491	Líquido comprimido	0,001009
3	212,4	2	2800	6,341	1	0,09963
4

Portanto, o calor transferido para a água representa toda a energia fornecida ao sistema pela fonte quente. Em função disso, teremos que:

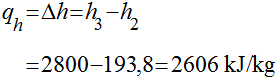
Finalmente, necessitamos calcular as propriedades termodinâmicas do estado 4. Considerando o condensador ideal, a perda de pressão será nula e, conseqüentemente, a pressão 4 será igual a pressão 1.

Além disso, considerando a turbina ideal, a variação de entropia entre os estados 3 e 4 é nula.

Ponto	Temperatura	Pressão	Entalpia	Entropia	Título	Volume
	°C	MPa	kJ/kg	kJ/kg/K		m3/kg
1	45,81	0,010	191,8	0,6492	0	0,00101
2	45,81	2	193,8	0,6491	Líquido comprimido	0,001009
3	212,4	2	2800	6,341	1	0,09963
4	45,81	0,010	2007	6,341	0,7588	11,13

Desta maneira, teremos que o trabalho realizado pela turbina será dado por:

 

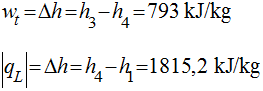
Com isto, completamos o cálculo de todos os estados termodinâmicos do ciclo e o rendimento será dado por: