Condutividade e Resistividade

Os materiais elétricos são muito utilizados no mundo atual.

Fios e cabos elétricos ligam as usinas de geração de energia a todos  equipamentos de uso final dos consumidores no planeta. A rede elétrica e telefônica  são os sistemas com maior capilaridade e extensão criados pelo homem.

Resistências transformam eletricidade em calor em diversos equipamentos e aplicações, tais como o chuveiro elétrico, o ferro de passar roupas, o secador de cabelos, a chapinha de alisamento, forno elétrico, fogão elétrico, etc..

Finalmente, resistências são indispensáveis ao funcionamento de equipamentos eletrônicos e de telecomunicações, tais como televisão, computador, telefone celular, etc...

A resistividade elétrica é a medida da resistência elétrica por quantidade de material e depende da composição e processo de fabricação do material.

Ela pode ser definida por volume ou por massa de acordo com as expressões abaixo:

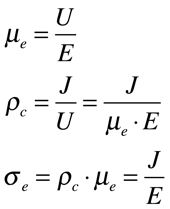
As expressões abaixo relacionam o campo elétrico, a velocidade das cargas, a mobilidade das cargas, a densidade de corrente elétrica com a condutividade do material considerando as questões anteriores.

A mobilidade das cargas é definida como sendo a velocidade das cargas dividida pelo campo elétrico.

A densidade de cargas elétricas é definida como sendo a densidade de corrente dividida pela velocidade das cargas.

Finalmente, a condutividade é definida como sendo da densidade de cargas multiplicada por sua mobilidade.

Onde:

1. •E é a intensidade do campo elétrico [V/m];
   

2. •U é a velocidade das cargas na direção da densidade de corrente [m/s];
   

3. •J é a densidade de corrente [A/m2];
   

4. •μe é a mobilidade das cargas [m2/(V.s)];
   

5. •ρc é a densidade de cargas elétricas [C/m3];
   

6. •σe é a condutividade do material [S/m];

Onde:

1. •δe é a resistividade elétrica por unidade de massa [Ω.kg/m2];
   

2. •ρe é a resistividade elétrica por unidade de volume [Ω.m].
   

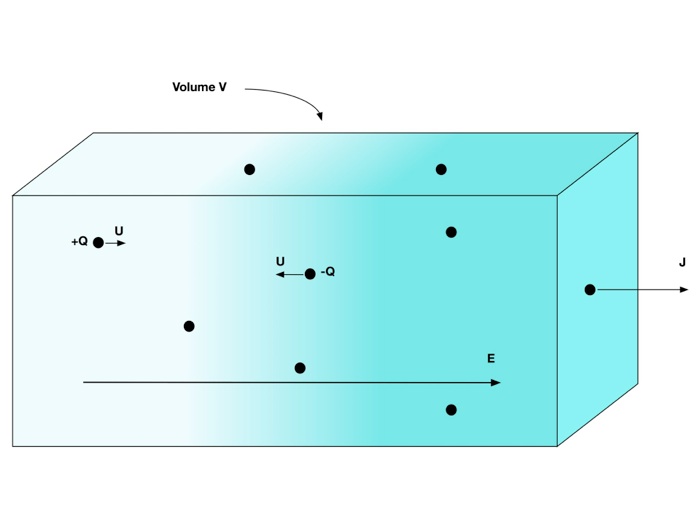
A figura abaixo mostra o efeito do campo elétrico nas cargas elétricas livres existentes no material.

Para que o material seja considerado condutor, é necessário a existência de corrente elétrica. Isto significa que as cargas elétricas devem ter velocidade. O campo elétrico é responsável pela força de aceleração das cargas. Porém, dependendo do material, um mesmo campo elétrico provoca diferentes velocidades.

Para resolver esta questão, criou-se o conceito da mobilidade das cargas, que depende do material. O conceito de mobilidade resolveu a questão das diferentes velocidades para campos iguais em materiais diferentes. Contudo não resolve a questão de densidades de corrente diferentes com velocidades de carga iguais em materiais distintos.

Para resolver esta questão, criou-se o conceito de densidade de cargas. Materiais com maior densidade de cargas livres permitem maiores densidades de corrente para um mesmo campo elétrico.

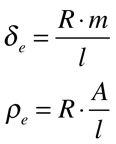
Resistividade dos Metais

Resistividade dos Metais

Fonte: Haynes, W.M., Handbook of Chemistry and Physics, 93 a Edição, CRC, 2012.

Medição de Resistividade

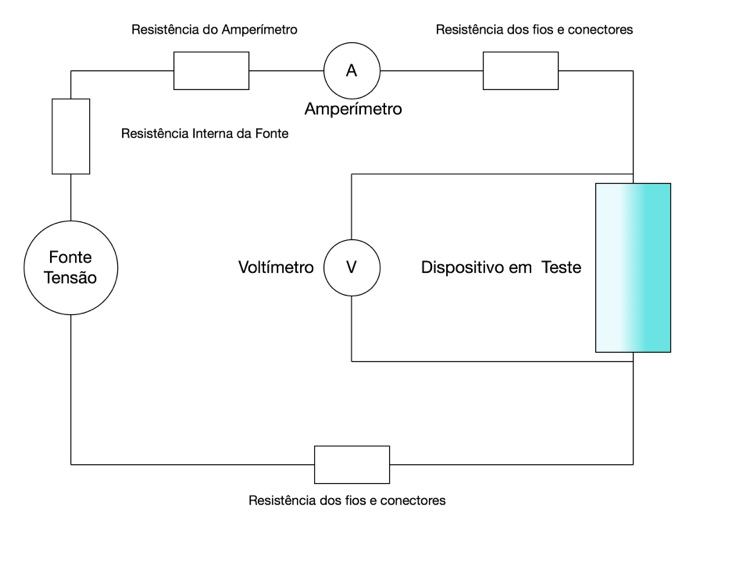
A medição de resistividade é feita pelo método do voltímetro e amperímetro. O método é aparentemente simples mas cuidados especiais devem ser tomados para que as medidas sejam as mais precisas possíveis.

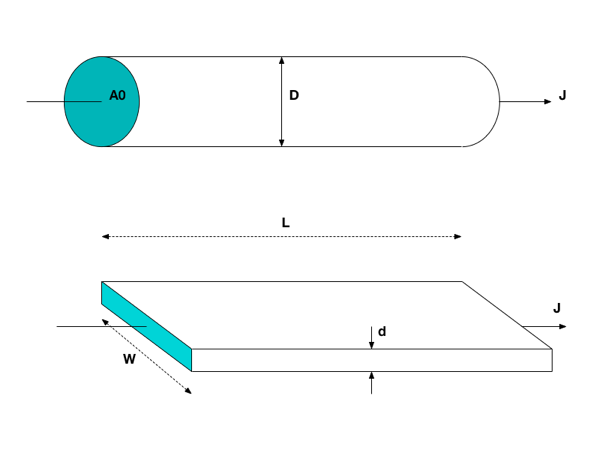
Conforme a figura abaixo, utiliza-se uma fonte de tensão contínua ajustável para gerar uma corrente no dispositivo em teste. Dependendo da resistência elétrica do dispositivo em teste, a resistência interna da fonte e as resistências dos fios utilizados na conexão não podem ser desconsideradas. Por isso, deve-se ligar o voltímetro o mais próximo possível do dispositivo em teste através de fios independentes da corrente principal.

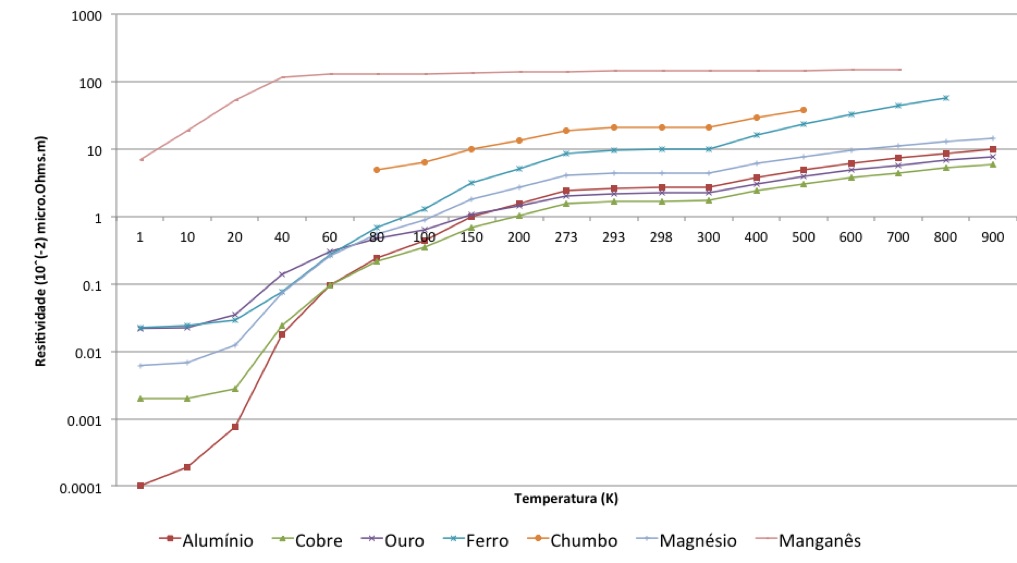
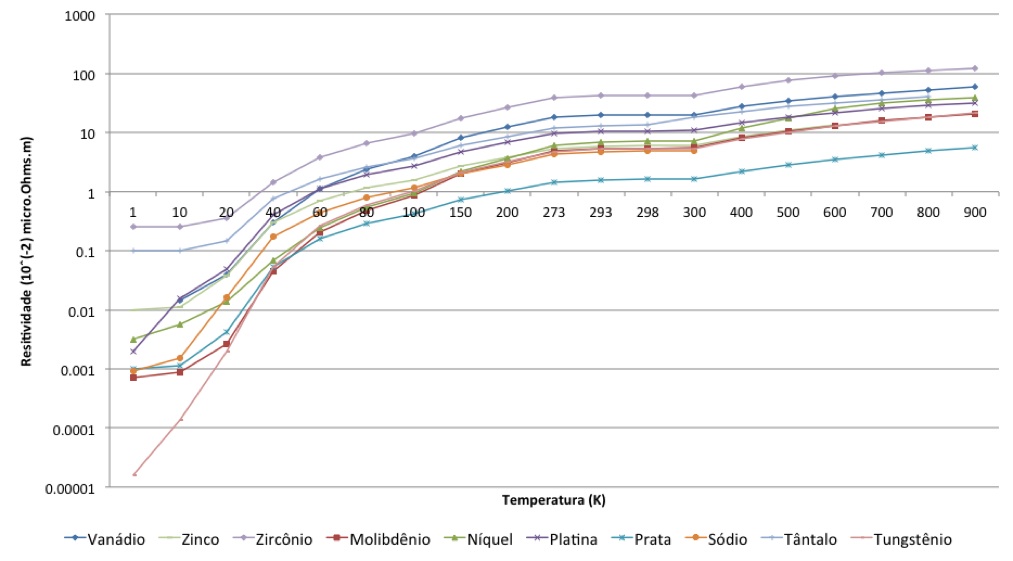
As figuras abaixo apresentam a resistividade de diversos metais em função da temperatura.

Observa-se que a resistividade de todos os metais apresentados varia de forma não linear com a temperatura. Contudo, a variação da resistividade é praticamente linear.

A variação da resistência devido à variação de temperatura é um problema prático em muitas aplicações da engenharia, tais como flecha de linhas de transmissão, ampacidade de fios e cabos, abertura de fusíveis, estabilidade térmica de resistores, etc...

Portanto, para a maioria dos problemas práticos, a resistividade elétrica de determinado material pode ser aproximada por:

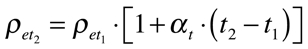
Onde:

αt é o coeficiente de variação da resistividade com a temperatura [1/°C];

t é a temperatura [°C] ;

ρe é a resistividade elétrica do material na temperatura t;

É importante ressaltar que esta equação não leva em consideração a dilatação do material devido à temperatura.

Os metais puros não são utilizados na prática porque sua obtenção é difícil e a existe sempre a dificuldade me manter a pureza dos materiais na prática. Por isso, a maioria dos condutores utilizados na prática são ligas sem 100% de pureza.

Observa-se das figuras abaixo que o cobre é o metal com menor resistividade depois da prata. Portanto, por questões econômicas, o cobre é o metal mais utilizado como condutor elétrico.

Por isso, o IACS - International Annealed Copper Standard - definiu a resistividade por unidade de massa do cobre recozido como sendo 0,15328 Ω.g/m2 e a resistividade por volume como sendo 1.7241 μΩ.cm, ambas  a 20 oC. Esses valores são conhecidos na prática como a resistividade de 100%.

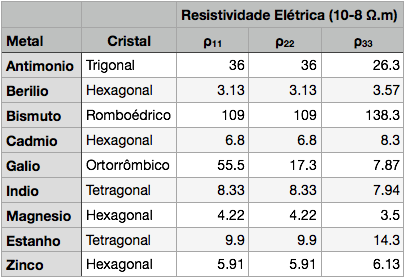
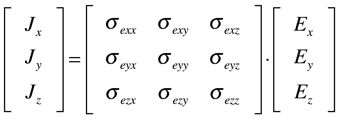
As expressões da densidade de corrente, campo elétrico e resistividade também podem ser escritas na forma tensorial. O campo elétrico e a densidade de corrente são tensores polares de primeira ordem e, consequentemente, a resistividade elétrica é um tensor polar de segunda ordem, conforme mostram as expressões abaixo.

É importante observar que a resistividade é o inverso tensorial (matricial) da condutividade. Isto significa que os elementos do tensor não são o inverso do elemento do outro tensor.

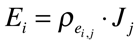
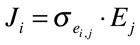
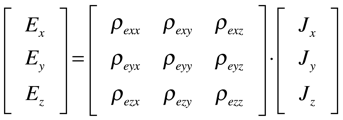
Dependendo das simetrias do material, a resistividade e a condutividade serão mais ou menos isotrópicas. A maioria dos metais são cúbicos e, consequentemente, a resistividade é isotrópica. A Prata é o metal com menor resistividade elétrica e é seguida pelo Cobre.

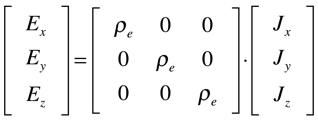
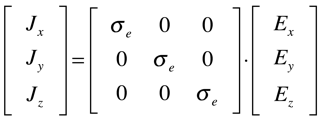
Cristais Cúbicos

Exemplos: Cobre, Alumínio, Prata, Ouro, Níquel, Paládio, Platina, Ferro, Manganês, Cromo, Molibdênio, Tungstênio, Vanádio, Nióbio, etc..

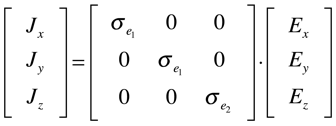
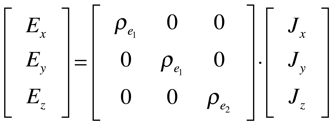
Cristais Uniaxiais

(Tetragonal, Trigonal, Hexagonal)

Exemplos: Titânio, Zircônio, Zinco, Cobalto, Mercúrio, etc..

Titânio

Cobalto

Cobre

Alumínio

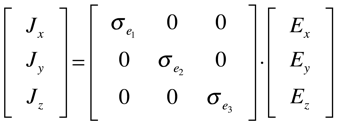
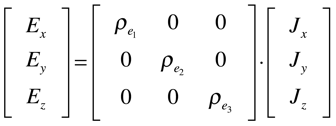
Cristais Ortorrómbicos

Exemplos: Gálio

Gálio

A Tabela abaixo apresenta a resistividade elétrica de alguns dos metais anisotrópicos.

Fonte: Newham, R. E., Properties of Materials - Anisotropy, Simetry, Structure, Oxford University Press, 2005.

Fonte: Newham, R. E., Properties of Materials - Anisotropy, Simetry, Structure, Oxford University Press, 2005.

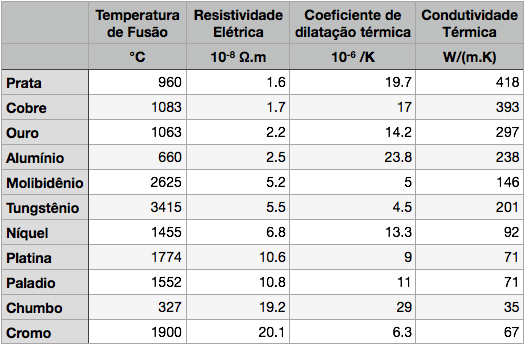
A Tabela abaixo mostra a a resistividade dos metais mais utilizados como eletrodos.

Observa-se que a prata é o metal com menor resistividade elétrica. Porém, seu elevado custo inviabiliza seu uso em grande escala como condutor elétrico.

O cobre é o segundo metal com menor resistividade elétrica e, por isso, é metal mais utilizado como condutor elétrico.

O terceiro metal com menor resistividade elétrica é o ouro e, pelo mesmo motivo da prata, é utilizado apenas em aplicações especiais.

O quarto metal com menor resistividade térmica é o alumínio e, por isso, ele divide com o cobre a colocação de metal mais utilizado como condutor de eletricidade.