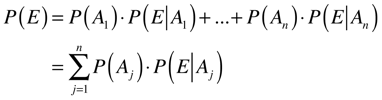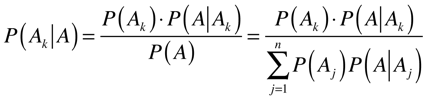Espaço de Amostragem

Espaço de amostragem – S - ou população é o conjunto de todos os pontos de amostragem, definidos como sendo os possíveis resultados de um experimento ou sistema randômico.

O espaço de amostragem pode ser:

1. •Contínuo;
   

2. •Discreto;
   

3. •Finitos;
   

4. •Infinitos.
   

Por exemplo, os conjuntos de todas as possíveis vazões de um rio, de todos os possíveis ventos em determinado ponto e de todos os possíveis preços de um combustível constituem espaços de amostragem contínuos e infinitos.

Por outro lado, o conjunto dos possíveis estados operacionais de uma usina é um exemplo de espaço amostragem discreto e finito.

Eventos

Evento é um subconjunto A do espaço de amostragem S. Quando este subconjunto é unitário ele é chamado de evento elementar ou simples.

Por exemplo, as vazões medidas em determinado ponto de um rio nos últimos 80 anos, os ventos medidos em determinada localidade nos últimos 10 anos e o preço do petróleo nos últimos 5 anos são Eventos dos respectivos Espaços de Amostragem.

Probabilidade

No caso de Espaços de Amostragem finitos, onde um evento – A - pode ocorrer de h maneiras diferentes de um total de n possibilidades diferentes e igualmente prováveis, a probabilidade P(A) é definida como sendo h/n.

Por exemplo, a probabilidade de um determinado número entre 1 e 60 ser sorteado na megasena é igual a 1/60.

Portanto, definir a probabilidade de eventos bem definidos pertencentes a espaços de amostragem também bem definidos é simples.

No entanto, qual a probabilidade do preço do petróleo ultrapassar U$100/barril ou a vazão em Itaipu ultrapassar 100m3/s?

Axiomas

1. 1.Para todo evento A, P(A)≥0, isto é, a probabilidade é sempre positiva.
   

2. 2.Para todo e qualquer evento A, 0≤P(A)≤1.
   

3. 3.P(A)=1 implica A é um evento certo.
   

4. 4.P(A)=0 implica que o evento A é impossível de ocorrer.
   

5. 5.Se o Evento A’ é o complemento de A, então P(A’)=1-P(A)
   

6. 6.O somatório ou a integral das probabilidades de todos os eventos de um espaço S é igual a 1.
   

7. 7.Para quaisquer dois eventos A e B, a probabilidade da união dos dois eventos é dada por:

I. Revisão

Conceitos Básicos

O que é Probabilidade?

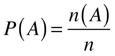
onde:

n(A) é o número de ocorrências do evento A;

n é o número total de eventos.

No limite, n tende N, o número total de eventos do espaço de amostragem da população. Quando isto ocorre, a definição acima converge para a probabilidade do evento.

Lei de Bayes

Supondo A1, A2,....., An, eventos mutuamente exclusivos cuja união forma o espaço de amostragem  S, isto é, um deles deve obrigatoriamente ocorrer, a Lei de Bayes diz que:

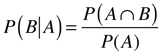
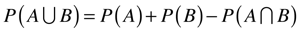
Probabilidade Condicional

Sejam A e B dois eventos de um espaço S com probabilidades maiores que zero. A probabilidade de B ocorrer dado que A ocorre é dada pela expressão abaixo.

Eventos Independentes

Z eventos são estatisticamente independentes se:

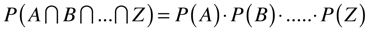
Distribuições de Probabilidade

As probabilidades dos eventos de determinado espaço de amostragem são normalmente descritas pela Função de Distribuição de Probabilidade -FDiP.

Em função das propriedades anteriores, a FDiP deve ser uma função crescente com valor mínimo igual a zero e máximo igual a 1.

Nos casos em que a FDiP é diferenciável, a Função de Densidade de Probabilidade - FDeP- é definida como a derivada da FDiP.

Álgebra de Conjuntos

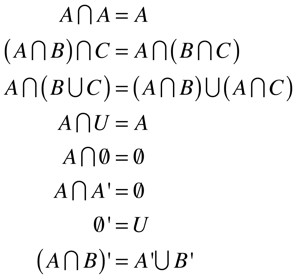
Lei da Probabilidade total

Supondo que E seja um evento do espaço S e A1,A2,...An sejam eventos mutuamente exclusivos, cuja união seja o espaço S, teremos que: