Constante Dielétrica e Perda Dielétrica

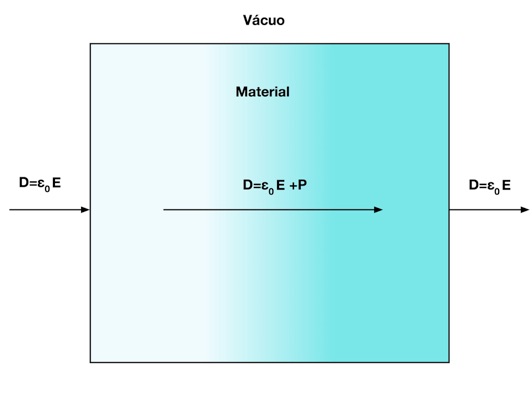
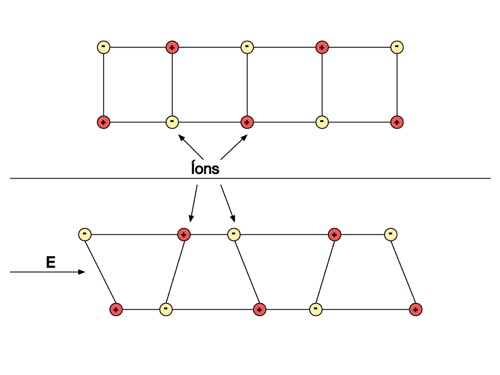
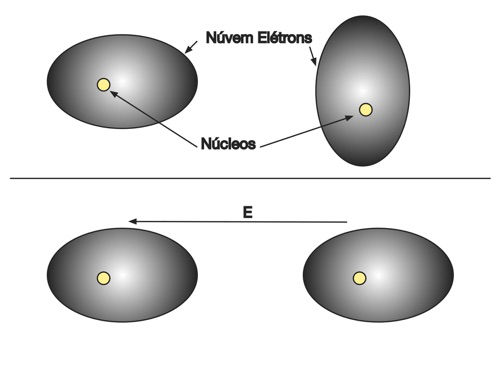
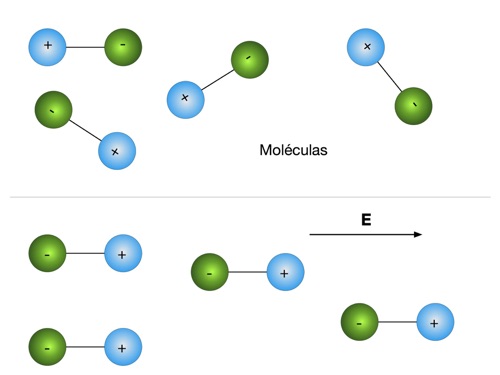
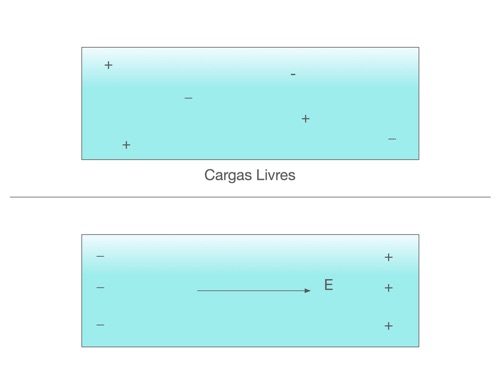
Dependendo da estrutura da matéria, o campo elétrico afetará a estrutura e o balanço das forças de atração e repulsão dentro dos materiais. As figuras abaixo apresentam a ação do campo elétrico nos átomos, ligações iônicas, moléculas e metais. Observa-se que em todos os casos, o campo elétrico externo produz um alinhamento das cargas elétricas existentes no material de modo que o campo elétrico no interior do material se modifica.

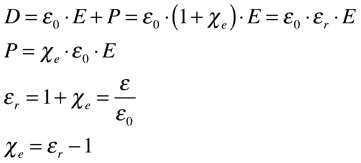
Onde:

1. • D é a densidade do fluxo elétrico [C/m2];
   

2. • P é o vetor de polarização [C/m2];
   

3. • E é a intensidade do campo elétrico [V/m];
   

4. • ε é a permissividade elétrica ou constante dielétrica do material [F/m];
   

5. • ε0 é a permissividade ou constante dielétrica do vácuo [8,854.10-12 F/m];
   

6. • εr é a permissividade ou constante dielétrica relativa do material;
   

7. • χe é a susceptibilidade elétrica do material.

As expressões acima podem ser escritas na forma tensorial de acordo coma expressão a abaixo. Observa-se que a Densidade de Fluxo Elétrico e a Intensidade de Campo Elétrico são tensores de primeira ordem e, consequentemente, a Constante Dielétrica dos materiais é um tensor de segunda ordem simétrico com as seguintes peculiaridades:

1. • os elementos diagonais são positivos;
   

2. • os elementos fora da diagonal podem ser negativos;
   

3. • os elementos fora da diagonal são menores, em módulo, do que os elementos da diagonal;
   

4. • os elementos são números complexos;
   

5. • os elementos variam com a frequência do campo elétrico porque, dependendo do tipo de carga, elas podem se orientar mais rapidamente ou não;
   

6. • a parte imaginária está associada à perda de energia que ocorre com a movimentação das cargas.
   

7. • a parte real e imaginária da constante dielétrica podem ter comportamentos e simetrias distintos com a frequência.

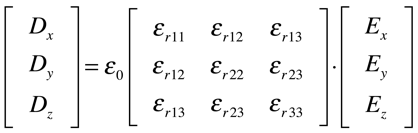
A Constante Dielétrica ou Permissividade Elétrica Relativa -εr - é a medida da capacidade do material de armazenar cargas elétricas e traduz, de forma macroscópica, os efeitos mostrados nas figuras acima. Ela varia em mais de 4 ordens de magnitude nos materiais isolantes.

Nos gases, em decorrência da baixa densidade, a constante dielétrica é um pouco maior do que um. Por exemplo, a constante dielétrica do ar na pressão de 1 atm é igual a 1,0006.

A maioria das cerâmicas e polímeros tem constante dielétrica na faixa entre 2 e 10, em função das ligações covalentes.

No caso de materiais com ligações iônicas, como o NaCl, a faixa situa-se entre 6 e 10. Materiais com elevados valores de constante dielétrica possuem mecanismos especiais de polarização que envolvem a rotação de dipolos ou transformação ferroelétrica de fase. A água, com constante dielétrica de 80 e o BaTiO3 (1000) são exemplos desses mecanismos.

O primeiro mecanismo mostrado nas figuras acima envolvendo as nuvens de elétrons existe em todos os materiais. Os outros mecanismos estão relacionados com o tipo de material envolvido.

Outro aspecto importante de ser observado é a diferença de massas e forças envolvidas nos quatro casos. Como a massa dos elétrons é muito pequena, a polarização elétrica ocasionada por eles responde a campos elétricos de alta frequência até a luz visível.

Por outro lado, como os íons são muito mais pesados do que os elétrons, a polarização iônica é sensível apenas até frequências próximas ao infravermelho.

Seguindo este raciocínio, as moléculas são mais pesadas que os íons e a polarização é sensível apenas até as microondas.

Finalmente, a polarização causada pela carga especial é sensível até a frequência de kilohertz.

O Eletromagnetismo explica de forma macroscópica este fenômeno,  de acordo com a figura abaixo, através do vetor de Polarização - P - de acordo com as expressões abaixo:

A simplificação do tensor constante dielétrica depende da estrutura e da simetria do material, conforme as expressões abaixo.

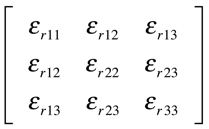
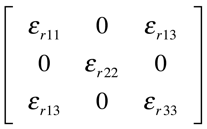
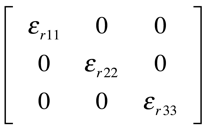
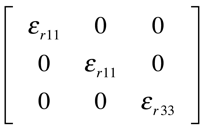
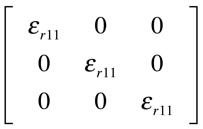
Cristais Triclínicos

Exemplo : Wollastonita - CaSiO3

Cristais Monoclínicos

Exemplo: Gipsita - Ca(SO4).2H2O

Cristais Ortorrômbicos

Exemplo: Bertrandita - Be4Si2O7(OH)2

Cristais Cúbicos

Exemplo : Galena - PbS

Cristais Uniaxiais

(Tetragonal, Trigonal, Hexagonal e Grupo de Curie)

Exemplo - Zircão - ZrSiO4

Bertrandita do Brasil

Wollastonita

Gipsita

Zircão do Brasil

Fonte Fotos: wikipedia.org

A constante dielétrica é tudo menos uma constante. Ela depende da frequência, do campo elétrico, da temperatura, da pressão e de outras variáveis. Além disso, ela é uma grandeza complexa, possuindo uma parte real e outra imaginária, conforme as expressões abaixo.

Galena

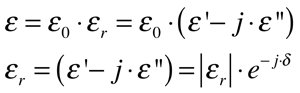
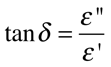
Onde:

1. •ε é a constante dielétrica do material [F/m];
   

2. •εr é a constante dielétrica relativa do material;
   

3. •ε0 é a constante dielétrica do vácuo [ 8,85x10-12 F/m];
   

4. •ε’ é a parte real da constante dielétrica relativa do material;
   

5. •ε” é a parte imaginária da constante dielétrica relativa do material;
   

6. •δ é o ângulo de perdas do material;
   

7. •tan(δ) é o fator de dissipação do dielétrico;
   

8. •σ é a condutividade do dielétrico [S/m];
   

9. •ω é a frequência [rad/s].

Capacitância

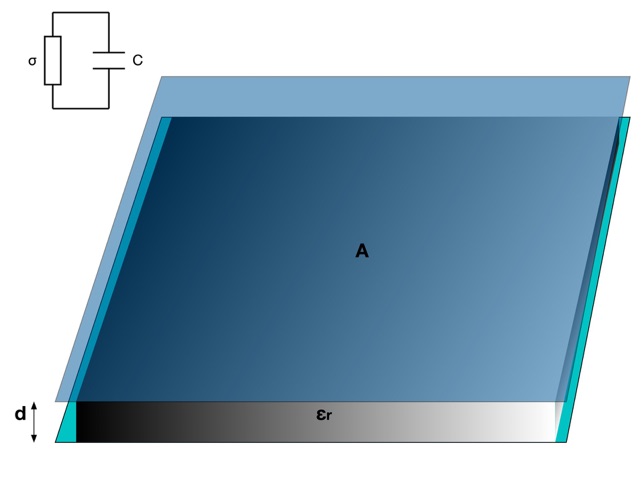
A capacitância de duas placas paralelas pela expressão abaixo, onde:

1. •C é a capacitância [F];
   

2. •A é a área das placas [m2];
   

3. •d é a distância entre as placas [m];
   

Esta expressão é aproximada porque despreza os efeitos das bordas no campo elétrico entre as placas.

Observa-se que o material entre as placas paralelas pode ser representado por um capacitor em paralelo com um resistor.

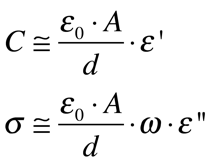
Cargas

Átomos

Moléculas

Íons

Micro-onda

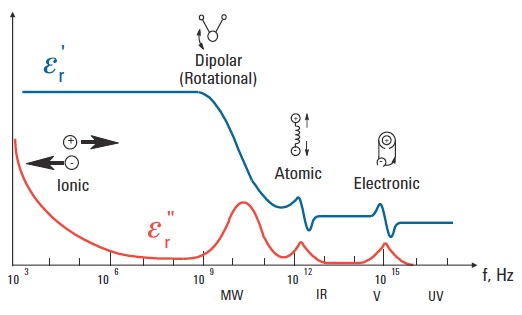
A variação da constante dielétrica com a frequência depende das ligações químicas predominantes no material, conforme mostra a figura abaixo.

Observa-se que a parte real da constante dielétrica permanece praticamente constante até as frequências de micro-ondas. Contudo, a parte imaginária, que está associada com as perdas, diminui até as frequências de micro-ondas e depois apresenta um aumento.

Fonte: Agilent Technologies, Basics of Measuring the Dielectric Properties of Materials - Application Note, site.

Dependendo da aplicação, existem os seguintes métodos de medição:

1. •Pontes de impedância;
   

2. •Transmissão/Reflexão de ondas;
   

3. •Ressonância;
   

4. •Linha de Transmissão.

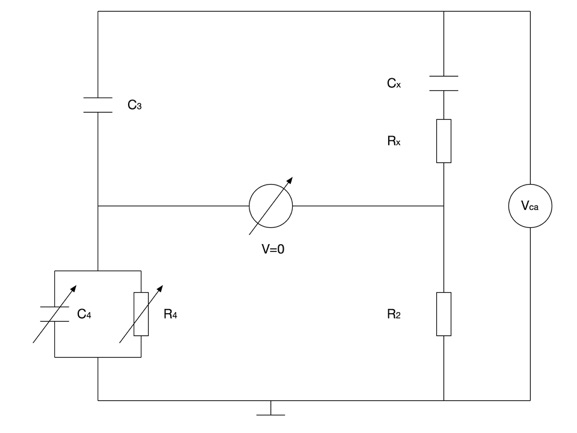
Ponte de Schering

A Ponte de Schering é utilizada para medições de capacitâncias e, indiretamente a constante dielétrica,  para frequências entre 0 até 10 MHz. A capacitância Cx é medida através do ajuste da resistência R4 e o fator de dissipação pelo ajuste de C4.

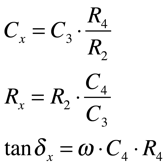
Forno de Micro-ondas

O forno de micro-ondas é a aplicação prática da constante dielétrica mais conhecida na vida cotidiana moderna. Capacitores são mais importantes porque estão presentes na maioria dos equipamentos elétricos e eletrônicos mas não são visíveis ao público leigo.

O forno de micro-ondas consiste basicamente numa fonte de ondas eletromagnéticas de frequência fixa ( ⋍2,4 GHz ) que, ao se propagar através dos materiais, produz aquecimento.

Todos nós sabemos que não se deve colocar qualquer material no forno de micro-ondas. Além disso, sabemos que alimentos diferentes comportam-se de forma distinta no forno. Como explicar teoricamente este conhecimento empírico?

O campo elétrico de uma onda eletromagnética plana e uniforme propagando em um material dielétrico homogêneo e isotrópico será dada por:

Medição da Constante Dielétrica da Água

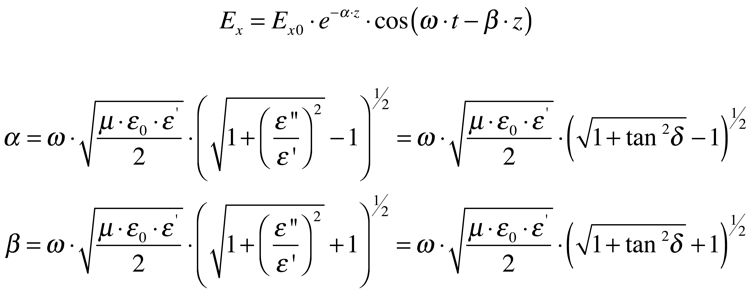
A profundidade de penetração, definida como sendo o inverso da constante de atenuação, representa a distancia percorrida pela onda eletromagnética para que a amplitude do campo elétrico diminua 63% (1/e). Isto significa que ela mede a capacidade de penetração de determinada onda eletromagnética no material em questão.

A densidade de potência dissipada no material é dada pela expressão abaixo e, analogamente ao campo elétrico, defini-se a profundidade de penetração de potência como sendo a metade da profundidade de penetração do campo elétrico. Isto significa que, dependendo da constante dielétrica do material e da frequência da onda eletromagnética, o aquecimento ocorrerá de forma diferente.

Onde:

1. •α é o fator de atenuação [1/m];
   

2. •β é a constante de fase [1/m].
   

O comprimento de onda - λ - e a impedância intrínseca - η - serão dados por:

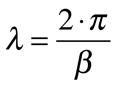
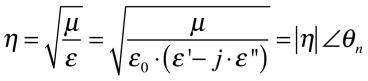
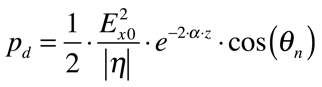
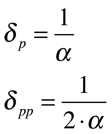
Experiências com Forno de micro-ondas